
|

|

|
 |
 |

| Propósito de la sesión. Conocer y
practicar la técnica para multiplicar
decimales.
Organización del grupo. A excepción de la última actividad de la sesión todas las demás pueden trabajarse en parejas. |
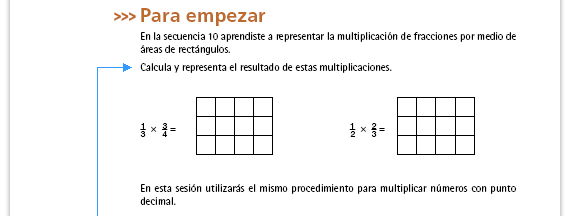
| Sugerencia didáctica. El modelo de
áreas para resolver una multiplicación
de fracciones se retoma para la
multiplicación de números con punto
decimal. Comente con los alumnos
este modelo y cerciórese de que lo
han comprendido antes de pasar al
Consideremos lo siguiente.
Respuestas. Para el primer caso se toma el ultimo renglon y las tres primeras columnas. La interseccion son 3 cuadros de los doce en total ( 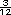 ) En el segundo caso se toman los
dos ultimos renglones y dos de las
columnas. La interseccion son 4 de los
doce ) En el segundo caso se toman los
dos ultimos renglones y dos de las
columnas. La interseccion son 4 de los
doce 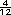 |

Propósito de la actividad. Pretende
que los alumnos den sentido al
resultado de la multiplicacion
representando en el cuadrado un
rectangulo que tenga por lados 0.48
y 0.6 Se espera que interpreten el
area del rectangulo (0.288) como
288 milesimos del cuadrado. Podrían
escribirlo como 2 880 diezmilesimas,
 o 0.2880. Es probable que
algunos sepan que estos números
son equivalentes a 0.288, si nadie
en el grupo llega a este resultado,
durante la confrontacion usted puede
recordárselos. o 0.2880. Es probable que
algunos sepan que estos números
son equivalentes a 0.288, si nadie
en el grupo llega a este resultado,
durante la confrontacion usted puede
recordárselos.
Respuestas. Es un cuadrado de 100 x 100, en total hay 10 000 cuadritos, asi que cada cuadrito es 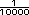 . Cada
renglón o columna de cuadritos es
igual a . Cada
renglón o columna de cuadritos es
igual a 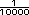 100 = 100 = 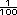 . Para
hacer la multiplicacion se toman
48 renglones de un lado ( . Para
hacer la multiplicacion se toman
48 renglones de un lado ( 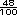 ), y del
otro se toman 60 columnas ( ), y del
otro se toman 60 columnas ( 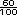 ). La
interseccion es de 2 880 cuadritos, es
decir, ). La
interseccion es de 2 880 cuadritos, es
decir,  o 0.288 o 0.288
Posibles dificultades. Si los alumnos no pueden resolver la actividad:
Y hacer preguntas similares para 0.48 |

Sugerencia didáctica. Durante la
confrontación enfatice que:
|
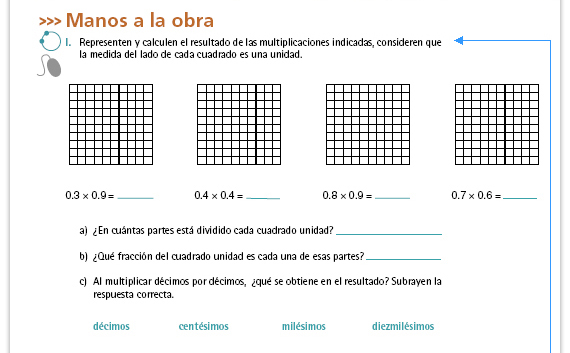
| Propósito de la actividad. Todas las
actividades de la sección Manos a la
obra están encaminadas a construir un
algoritmo para multiplicar decimales.
En la actividad I se pretende que
el alumno deduzca que multiplicar
décimos por décimos da centésimos y
que lo visualice gráficamente en los
recuadros.
Respuestas. Cada cuadrado es de 10 x 10 y en total hay 100 cuadritos, asi que cada cuadrito es 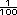 . Para
resolver el primer ejercicio, por
ejemplo, se toman 3 reglones
(30 cuadritos = . Para
resolver el primer ejercicio, por
ejemplo, se toman 3 reglones
(30 cuadritos = 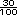 ), y 9 columnas
(90 cuadritos = ), y 9 columnas
(90 cuadritos = 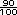 ). El resultado son
27 cuadritos, es decir, ). El resultado son
27 cuadritos, es decir, 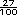 o 0.27 o 0.27 |
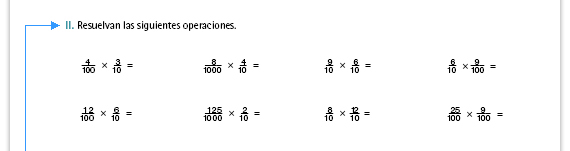
| Sugerencia didáctica. En la secuencia 10 se estudió la multiplicación de fracciones, así que se espera que los alumnos puedan resolver esta actividad. Para lograr el vínculo con la actividad III, aclare a los alumnos que no es necesario simplificar el resultado. |

Para recordar. Una fracción con
denominador 10, 100, 1 000 puede
expresarse también con un número
con punto decimal:
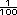 se lee un décimo y puede escribirse
como 0.1 se lee un décimo y puede escribirse
como 0.1
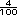 se lee cuatro centesimos y puede
escribirse 0.04 se lee cuatro centesimos y puede
escribirse 0.04
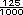 se lee ciento veinticinco milesimos
y puede escribirse 0.125 se lee ciento veinticinco milesimos
y puede escribirse 0.125
Cuando las cifras no alcanzan para poner el punto en el lugar adecuado entonces se completa con ceros. Por ejemplo, para cuatro centésimos se requieren dos lugares y el 4 sólo tiene una cifra, por ello se escribe un cero entre el punto y el cuatro: 0.04 Sugerencia didáctica. Escriba en el pizarrón algunos de los números de las multiplicaciones y pida a los alumnos que los lean. También puede pedirles que los escriban en forma de fracción. Por ejemplo: 0.04 "cuatro centésimos" 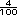
Si nota que muchos alumnos tienen dificultades, es conveniente hacer algunos ejercicios como éste de manera grupal. |
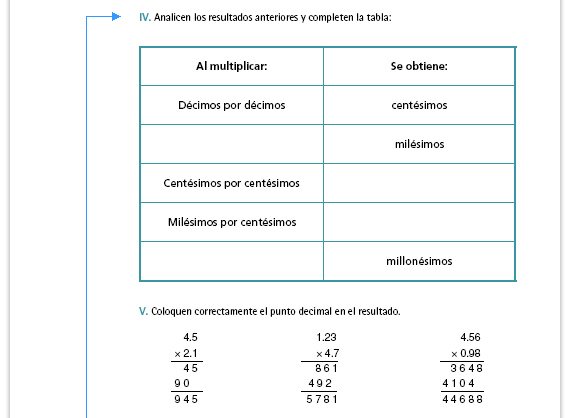
| Posibles dificultades. Si nota que
a los alumnos les cuesta trabajo
llenar la tabla, invítelos a analizar las
multiplicaciones que acaban de hacer.
Respuestas. Para los millonésimos hay varias soluciones, por ejemplo, décimos por cienmilésimos y milésimos por milésimos. |

 Sugerencia didáctica. Es muy común
que los alumnos sepan más de lo que
pueden expresar, sobre todo si es por
escrito. No se preocupe si escriben
algo que no es completo o correcto,
con la práctica podrán, poco a poco,
desarrollar esta habilidad.
Sugerencia didáctica. Es muy común
que los alumnos sepan más de lo que
pueden expresar, sobre todo si es por
escrito. No se preocupe si escriben
algo que no es completo o correcto,
con la práctica podrán, poco a poco,
desarrollar esta habilidad.
Invite a varios alumnos a que lean lo que anotaron y comenten qué reglas son correctas y cuál es la que se entiende mejor. |

| Sugerencia didáctica. El manejo de técnicas es otro de los propósitos de la enseñanza de las matemáticas, por ello se incluyen ejercicios para que el alumno practique la técnica aprendida. Si lo cree necesario puede poner más operaciones para que los alumnos las resuelvan en su cuaderno. Si quiere enriquecer la actividad se sugiere que elija una operación e invite a los alumnos a que inventen un problema que se resuelva con ella. Es un ejercicio interesante que apela a la creatividad del alumno y contribuye a su comprensión de la operación en juego. |

 Sugerencia didáctica. Repase
con los alumnos esta información
y de ser necesario resuelvan más
multiplicaciones (los alumnos pueden
proponerlas).
Enfatice la regla de completar con
ceros cuando sea necesario.
Sugerencia didáctica. Repase
con los alumnos esta información
y de ser necesario resuelvan más
multiplicaciones (los alumnos pueden
proponerlas).
Enfatice la regla de completar con
ceros cuando sea necesario. |
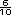 en
uno de los lados del cuadrado?
en
uno de los lados del cuadrado?