Propósito de la sesión. Reconocer a la mediatriz de un segmento como la perpendicular que pasa por el punto medio del segmento, como el eje de simetría del segmento y como el lugar geométrico de los puntos que equidistan de los extremos del segmento. Organización del grupo. El problema inicial se resuelve en equipos y la sección Manos a la obra de manera individual. Materiales. Juego de geometría (para las tres sesiones de toda la secuencia).

Propósito de la actividad. Se espera que los alumnos se familiaricen con la representación gráfica y con la ubicación de algunos puntos. Las respuestas pueden obtenerse únicamente mediante la observación, aunque es probable que algunos alumnos midan para ser más precisos. Posibles procedimientos.La mayoría encontrará el punto medio del segmento que determinan las casas de Ara y Bety, con la idea de que Carlos vive a la mitad del camino entre ambas casas; para ello, es muy probable que utilicen la regla. Es difícil que consideren otros puntos que también se encuentran a la misma distancia de ambas casas; probablemente ubicarán esos otros puntos por aproximación, midiendo con su regla.

Eje

Forma, espacio y medida.

Tema

Significado y uso de las operaciones.

Antecedentes

Para trabajar con esta secuencia los alumnos requieren del apoyo de algunos conceptos geométricos, por ejemplo: recta, semirrecta y segmento. Es conveniente que en los momentos en los que se haga uso de esos conceptos se dé un tiempo breve para repasarlos o recordarlos. Asimismo, se requieren ciertos procedimientos que los alumnos utilizaron en la secuencia 5: medición de ángulos, trazo de perpendiculares y medición de la distancia de un punto a una recta.

Propósitos de la secuencia Que los alumnos utilicen las propiedades de la mediatriz de un segmento y la bisectriz de un ángulo para resolver diversos problemas geométricos
Sesión	Título y propósitos de la sesión	Recursos
1	A la misma distancia Reconocer a la mediatriz de un segmento como la perpendicular que pasa por el punto medio del segmento, como el eje de simetría del segmento y como el lugar geométrico de los puntos que equidistan de los extremos del segmento.	Interactivo
2	Un problema geométrico Reconocer a la bisectriz de un ángulo como la semirrecta que pasa por el vértice del ángulo y lo divide en dos iguales, como el eje de simetría del ángulo y como el lugar geométrico de los puntos que equidistan de los lados del ángulo.	Interactivo Video "Mitades de ángulos"
3	Apliquemos nuestros conocimientos de mediatrices y bisectrices Aplicar las propiedades de la mediatriz y la bisectriz en la resolución de diversos problemas.

Propósito de las actividades. En este apartado se presenta un procedimiento sistemático para obtener puntos que están a la misma distancia de A y de B; la presentación de este procedimiento va acompañada de preguntas para que los alumnos reflexionen sobre él. Durante la confrontación de respuestas invite a los alumnos a que argumenten por qué el procedimiento descrito es o no correcto.

Sugerencia didáctica. Es importante que los alumnos vayan incorporando a su vocabulario algunos términos geométricos: "equidistan", "extremos", "mediatriz", "recta" y "segmento". Aproveche distintos momentos de la clase para recordar o aclarar el significado de cada término.

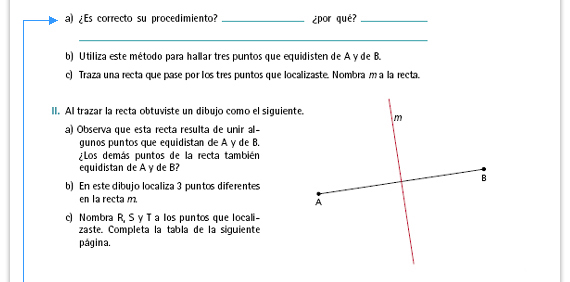
Posibles respuestas. El procedimiento sí es correcto, pero para los alumnos puede resultar difícil argumentar por qué. Algunas posibles respuestas son: "Porque los radios son iguales", "Porque están a la misma distancia", "Porque A y B son los centros de las circunferencias". Anime a los alumnos a expresar sus argumentos.

Respuestas: Las distancias indicadas en ambas columnas deben ser iguales.

Propósito de la actividad. La preguntas g y h tienen como propósito que los alumnos se den cuenta de la relación que guardan entre sí varios conceptos matemáticos; en este caso identificarán que la mediatriz de un segmento es la perpendicular que pasa por el punto medio del segmento y, además, es su eje de simetría. Sugerencia didáctica. Anímelos a que argumenten la idea anterior. Es probable que sus respuestas al inciso h sean muy limitadas: "Por que sí", "Porque se ve", "Porque es el eje de simetría". Motívelos para que incluyan más argumentos que involucren lo estudiado en las lecciones de simetría, por ejemplo: "Porque la recta es como un espejo en el que la mitad del segmento se refleja del otro lado"; "Porque al doblar por la recta el punto A y el B coinciden"; o bien, "Porque el punto A y B equidistan del eje y el segmento que los une es perpendicular a él".

Es importante que los alumnos desarrollen la habilidad de interpretar instrucciones escritas para hacer trazos geométricos, pero esa habilidad se desarrolla gradualmente. Anímelos a interpretar la información y evite sustituir su esfuerzo por las explicaciones que usted podría dar. El tiempo invertido en el esfuerzo de los alumnos podrá recuperarse cuando se enfrenten nuevamente a una situación similar.

Propósito de la actividad. El "Manejo de técnicas" es una de las habilidades que los alumnos deben desarrollar, para ello son necesarias actividades de ejercitación como ésta. Permita que los alumnos elijan entre los dos procedimientos que se les muestran para trazar la mediatriz.

Propósito de la actividad. Es importante que realicen esta actividad para comprobar su respuesta al problema inicial, pues es una manera de validar los procedimientos que hayan empleado.

Comisione a una pareja de alumnos para que elabore un cartel con la información que aquí se presenta. Ese cartel se pegará en el salón para que los alumnos puedan consultarlo cuando sea necesario. Lea y comente con el grupo esta información. Enfatice el hecho de que un mismo concepto matemático está relacionado con otros de diversas maneras. Posteriormente puede pedirles que copien la información en sus cuadernos.

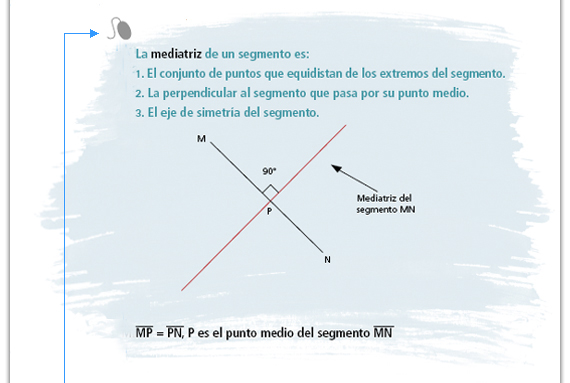
Propósito del interactivo. Explorar las propiedades de la mediatriz.