Propósito de la sesión. Reconocer a la bisectriz de un ángulo como la semirrecta que pasa por el vértice del ángulo y lo divide en dos iguales, como el eje de simetría del ángulo y como el lugar geométrico de los puntos que equidistan de los lados del ángulo. Organización del grupo. El problema inicial se resuelve en parejas y la sección Manos a la obra de manera individual.

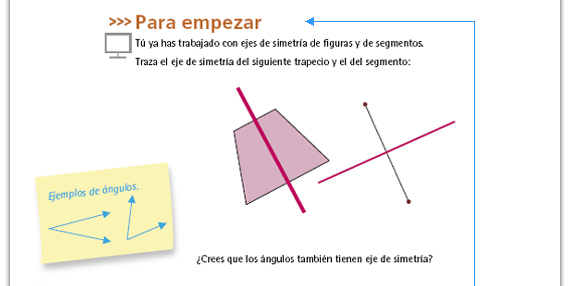
Propósito de la actividad. Recordar a los alumnos el trazo de ejes de simetría, lo que permitirá iniciar el estudio de la bisectriz como eje de simetría de un ángulo. Sugerencia didáctica. Si lo considera necesario, revise junto con los alumnos la sesión 2 de la secuencia 5, para recordar el trazo de ejes de simetría.

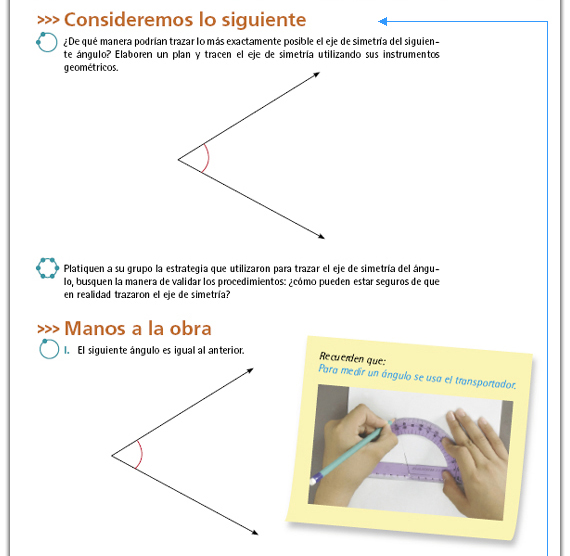
Posibles procedimientos. La indicación de que deben usar sus instrumentos geométricos para trazar el eje de simetría impide que recurran al doblado de la hoja por la mitad o que se orienten simplemente por la percepción visual; no obstante, pueden recurrir a otros procedimientos: medir la distancia que hay entre dos puntos (uno de cada lado del ángulo, procurando que estén a la misma distancia del vértice) y ubicar el punto medio de esa distancia; o bien, uniendo con un segmento las dos puntas de flecha (formando un triángulo), medir ese segmento y ubicar el punto medio. El eje partiría del vértice y cortaría el segmento por su punto medio. Otros podrían utilizar el transportador para medir el ángulo y partirlo por la mitad. Sugerencia didáctica. Motive a los alumnos para que platiquen sus procedimientos y para que ellos mismos los validen. En la actividad V del apartado Manos a la obra hallarán una manera de saber si trazaron correctamente el eje de simetría.

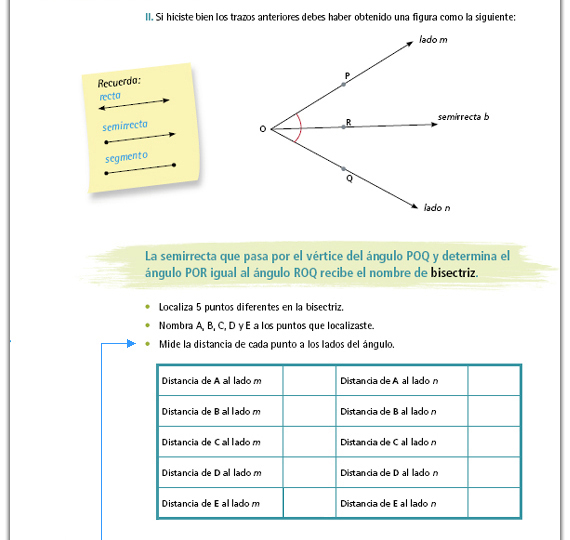
Sugerencia didáctica. En la medida que los alumnos avancen en el estudio de la geometría tendrán que incorporar nuevos términos y, sobre todo, hallar relaciones y diferencias con otros términos que ya estudiaron. En este momento es importante comentar con los alumnos la diferencia entre recta, semirrecta y segmento. Puede hacerlo cuando los alumnos estén resolviendo esta parte o al momento de la confrontación de las respuestas.

Posibles respuestas. Para la pregunta d, es probable que los alumnos no den argumentos matemáticos; invítelos a que recuerden lo estudiado en la secuencia 5 sobre simetría y que verifiquen con ello si la semirrecta b es o no eje de simetría. Algunos argumentos posibles son: "Cada punto tiene a su simétrico del otro lado"; "La semirrecta funciona como espejo"; "Divide al ángulo en dos ángulos de tal manera que cada uno es simétrico del otro".

Sugerencia didáctica. Recuerde a los alumnos que la distancia de un punto a una recta se mide por la perpendicular; de ser necesario, muestre en el pizarrón cómo se traza utilizando los instrumentos geométricos. Respuestas. Las distancias indicadas en ambas columnas de la tabla deben ser las mismas.

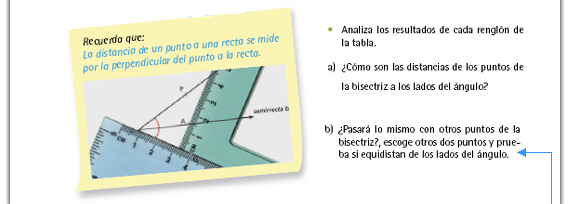
Propósito de la actividad. Los alumnos aún no están en posibilidades de hacer demostraciones para garantizar que esta propiedad se cumple en todos los casos; en este nivel es suficiente que prueben con varios puntos que ellos mismos elijan para llegar a la conclusión de que lo más probable es que esta propiedad se cumpla para todos los puntos de la bisectriz.

Propósito del interactivo. Observar paso a paso el procedimiento para trazar la bisectriz.

Permita que sean los alumnos quienes traten de interpretar las instrucciones escritas, posteriormente usted puede comentar al grupo esta secuencia de pasos para trazar una bisectriz.

Sugerencia didáctica. Recuerde que es importante que los alumnos desarrollen la habilidad de manejar técnicas. Si no da tiempo de llevar a cabo la actividad IV en la clase, puede dejarla como tarea.

Sugerencia didáctica. Motive a los alumno a que realmente comprueben si resolvieron correctamente el problema inicial, siguiendo el procedimiento que aquí se indica.

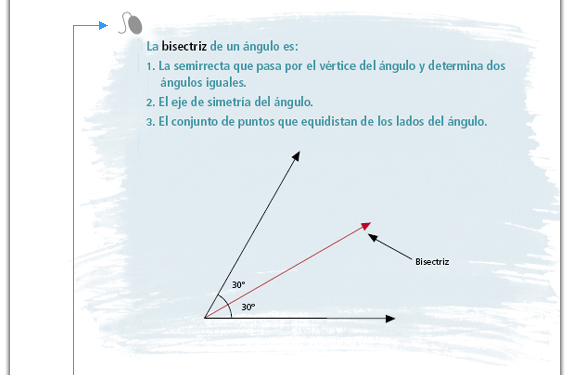
Comisione a una pareja de alumnos para que elabore un cartel con esta información. Lea y comente con el grupo esta información, puede ir verificando, junto con los alumnos, cada una de las definiciones de bisectriz. Puede pedirles que copien la información en sus cuadernos.

Propósito del interactivo. Explorar las propiedades de la bisectriz.

Propósito del video. Mostrar el trazo de la mediatriz y la bisectriz y plantear problemas diversos que las involucren.