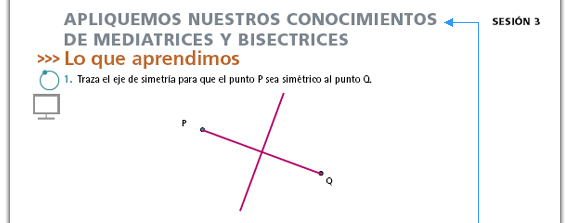
Propósito de la sesión. Aplicar las propiedades de la mediatriz y la bisectriz en la resolución de diversos problemas. Organización del grupo. Se sugiere que toda las actividades se trabajen de manera individual y que al final se comparen las respuestas y procedimientos con todo el grupo. Puede dejar algunas de las actividades de tarea (particularmente la 6 y la 7) para que los alumnos tengan más tiempo de explorar una posible solución.

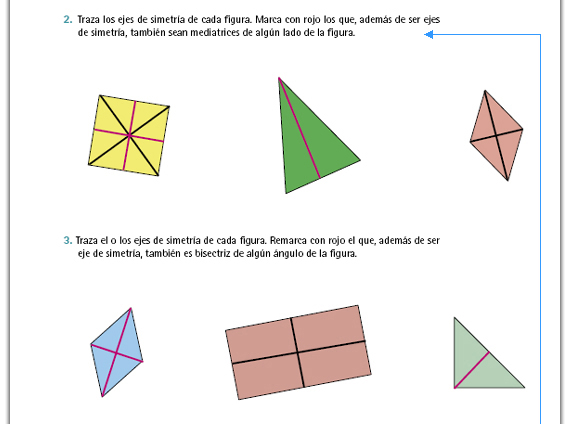
Propósito de las actividades. Las actividades 2 y 3 pretenden que los alumnos establezcan relaciones entre los conceptos de mediatriz y bisectriz por medio del concepto de eje de simetría.

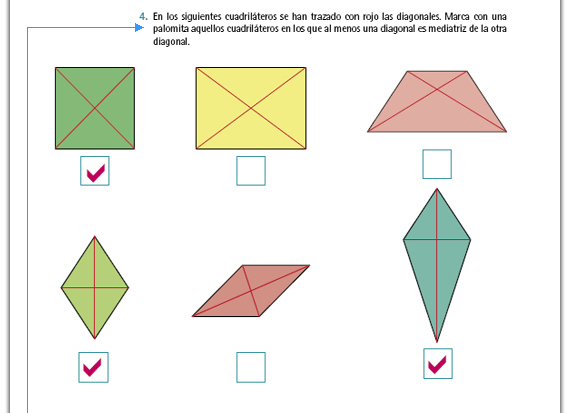
Sugerencia didáctica. Aun cuando los alumnos estudiaron las diagonales en la escuela primaria, es posible que no lo recuerden; si lo considera necesario recuerde a los alumnos lo que es una diagonal.

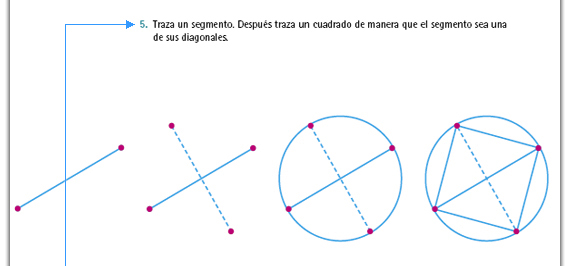
Respuesta. La clave para la resolución del problema es el trazo de la mediatriz: Se traza un segmento y, posteriormente, la mediatriz del segmento. Después, con centro en el punto donde se cortan las mediatrices y tomando como radio la distancia de ese centro a un extremo del segmento, se traza una circunferencia; en la circunferencia quedan marcados los cuatro vértices del cuadrado, al unirlos se forma el cuadrado. Los dibujos de la derecha ilustran ese procedimiento.

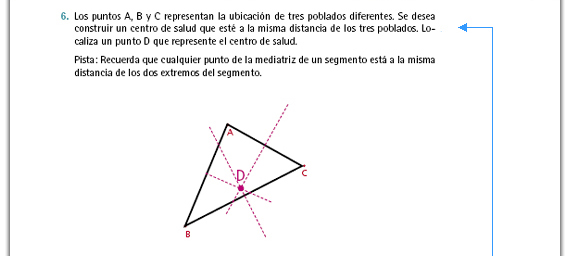
Incorporar al portafolios. La herramienta que permite resolver este problema es el trazo de las mediatrices de cada uno de los segmentos que unen a los puntos A, B y C. El punto en el que se unen las tres mediatrices es en donde va el centro de salud. La dificultad está en que los alumnos identifiquen que la equidistancia de los puntos que conforman la mediatriz es precisamente la característica que les permite resolver el problema. Si observa que los alumnos no consideran esa característica como parte de la solución del problema, repase con ellos las actividades número II del apartado Manos a la obra de la sesión 1. En caso de que sí identifiquen cómo se resuelve el problema, pero tengan dificultades para trazar las mediatrices, repase las actividades número III del Manos a la obra de la sesión 1.

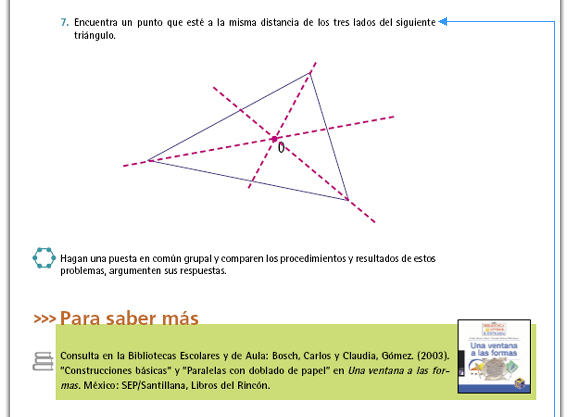
Incorporar al portafolios. Es un problema con un grado de dificultad similar al anterior, pero ahora con la bisectriz. Hay que trazar la bisectriz de cada uno de los ángulos del triángulo. El punto buscado es justamente donde se cortan las bisectrices. Si los alumnos no identifican que la equidistancia de los puntos que conforman la bisectriz es la característica que permite resolver el problema, repase las actividades número III del Manos a la obra de la sesión 2. Si la dificultad está en el trazo de las bisectrices, repase las actividades número III del apartado Manos a la obra de la sesión 2.