Propósito de la sesión. Construir polígonos regulares inscritos en una circunferencia a partir de la medida de su ángulo central. Organización del grupo. Se recomienda trabajar en parejas, y de manera individual la actividad VII de Manos a la obra Materiales. Juego de geometría, un pedazo de cartulina o de cualquier papel, tijeras y colores.

Propósito de la actividad. Se trata de hacer un breve repaso sobre las características que definen a un polígono regular; este repaso debe ser de manera breve y concisa, por lo que probablemente será necesario que usted intervenga para aclarar o corregir algunas ideas de los alumnos.

Propósito del video. Identificar a los polígonos regulares y utilizar sus propiedades para resolver problemas diversos.

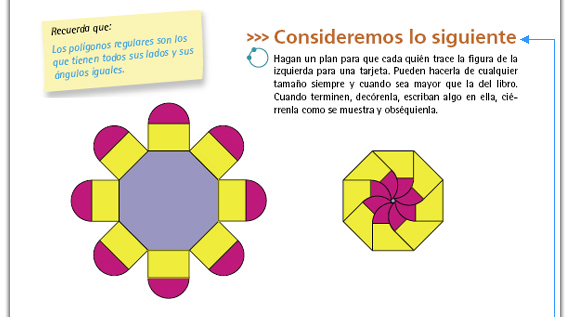
Propósito de la actividad. Se espera que los alumnos traten de trazar el octágono haciendo uso de sus propios procedimientos, no importa si éstos no son sistemáticos o formales. Sin embargo, la restricción de que la figura debe ser mayor que la del libro es para evitar que algunos alumnos la calquen y, de alguna manera, forzarlos a que traten de buscar otras estrategias. Posibles procedimientos. Una estrategia es dibujar un círculo y dividirlo con líneas en 8 partes más o menos iguales. Los puntos donde las líneas corten la circunferencia son los vértices. Otra opción es dibujar el octágono "al tanteo", sin tener mucho éxito porque hacerlo de este modo no es fácil. Puede ser que algunos midan los ángulos y los lados y traten de reproducirlo con estos datos, aunque la medida de los lados debe ser mayor a la del dibujo. No importa si en este momento no logran resultados óptimos.

Eje

Forma, espacio y medida.

Tema

Formas geométricas.

Antecedentes

Para trabajar con esta secuencia los alumnos deberán apoyarse en ciertos conceptos y procedimientos que han trabajado ya sea en la escuela primaria o en las secuencias 5 y 12: polígono regular, eje de simetría, ángulo, bisectriz, mediatriz, diagonal, y medición y trazo de ángulos.

Propósitos de la secuencia Que los alumnos construyan polígonos regulares a partir de distintas informaciones.
Sesión	Título y propósitos de la sesión	Recursos
1	Tarjetas de felicitación Construir polígonos regulares inscritos en una circunferencia a partir de la medida de su ángulo central.	Interactivo Video "Felicidades"
2	Mosaicos Construir polígonos regulares a partir de la medida de su lado y su ángulo interior.	Interactivo
3	Más sobre polígonos regulares Construir polígonos regulares a partir de informaciones como: ejes de simetría, ángulos centrales, ángulos interiores, etcétera.

Sugerencia didáctica. Durante la confrontación enfatice los trazos que cada equipo intentó. Lo importante en este momento es que analicen la figura, que traten de encontrar relaciones entre lados y ángulos y que desarrollen destreza en el uso de sus instrumentos geométricos.

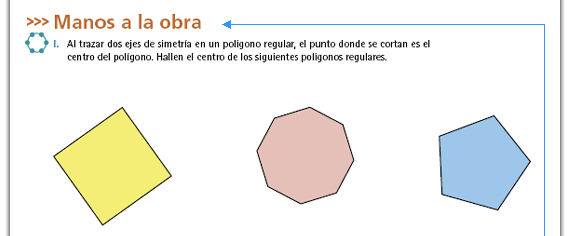
Propósito de las actividades. A lo largo de este apartado se presenta uno de los procedimientos para construir polígonos regulares: a partir del ángulo central. Por ello se hace primero una breve presentación de la noción de ángulo central y después se va desarrollando el procedimiento para la construcción de polígonos regulares.

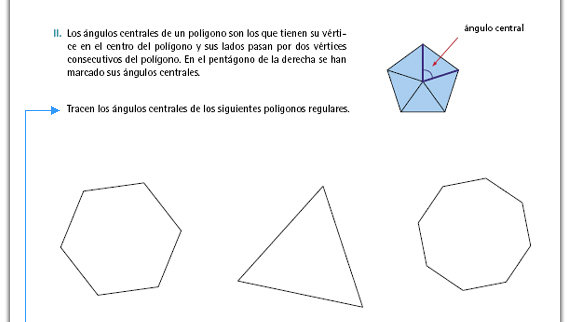
Sugerencia didáctica. Cerciórese de que cada pareja haya comprendido cuál es el ángulo central y que lo midan de manera correcta. Mientras observa el trabajo de los alumnos puede plantearles algunas preguntas que los hagan reflexionar: ¿En un mismo polígono regular todos los ángulos centrales miden lo mismo? (La respuesta es sí). En polígonos regulares con el mismo número de lados pero de diferente tamaño ¿los ángulos centrales medirán lo mismo? (La respuesta es sí).

Recuerde que.
Un polígono es una superficie limitada por lados rectos. Un polígono regular es aquel que tiene todos sus ángulos iguales y todos sus lados iguales.
Los siguientes rombos no son polígonos regulares, tienen sus lados iguales pero sus ángulos no.
Los siguientes rectángulos tampoco son polígonos regulares, tienen sus ángulos iguales pero sus lados no.

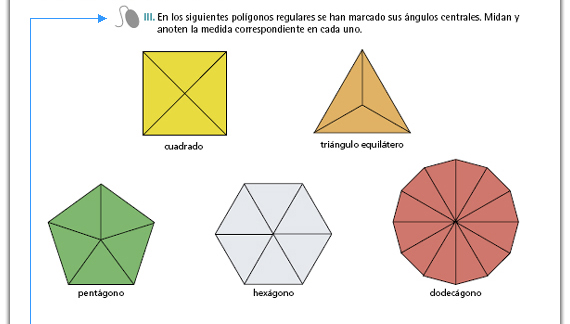
Propósito de las actividades III y IV: Explorar que la medida del ángulo central, multiplicada por el número de lados de un polígono regular, siempre da 360º. Esto implica que: -Conocido el número de lados de un polígono regular puede calcularse la medida del ángulo central. -Conocida la medida del ángulo central de cierto polígono regular puede calcularse el número de lados del polígono.

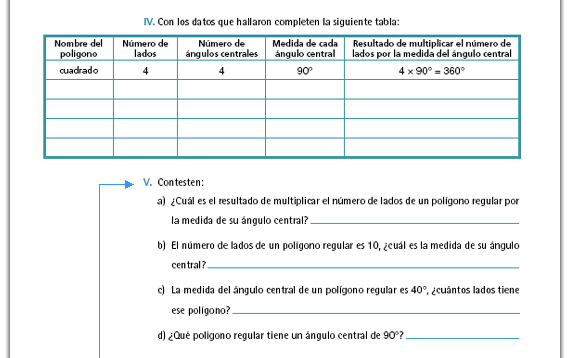
Repuestas. a) 360°. b) Es 36° porque el número de lados por la medida del ángulo central debe ser 360°, entonces 10 × 36° = 360°. c) Tiene 9 lados, porque 9 × 40° = 360° d) Es el cuadrado: tiene 4 lados, 4 × 90° = 360°.

Sugerencia didáctica. Durante la confrontación de resultados ponga énfasis en las ideas que anteriormente se comentaron: la medida del ángulo central multiplicada por el número de lados de un polígono regular siempre da 360º; lo cual implica que: -Conocido el número de lados de un polígono regular puede calcularse la medida del ángulo central. -Conocida la medida del ángulo central de cierto polígono regular puede calcularse el número de lados del polígono.

Es importante desarrollar en los alumnos las habilidades de leer e interpretar las técnicas para hacer trazos geométricos, por lo que es conveniente que traten de reproducir en sus cuadernos lo que se les indica en las instrucciones y en las imágenes. En un segundo momento, algunos alumnos pueden mostrar al grupo en el pizarrón cómo hicieron los trazos.

Propósito de la actividad. Que los alumnos practiquen la técnica aprendida. Sugerencia didáctica. Los alumnos pueden trazar en la clase una o dos figuras y el resto pueden hacerlas en casa como tarea. Pídales que sigan el procedimiento descrito y que consideren que la circunferencia que dibujen debe ser lo suficientemente grande en los casos de 10 y 12 lados, para que los trazos puedan hacerse con mayor facilidad. Si decide realizar los trazos de otros polígonos regulares por medio de esta técnica, deberá tener en cuenta que únicamente funciona con polígonos cuyo número de lados es un divisor de 360. Sería conveniente solicitar que tracen, por ejemplo, un heptágono, para que los mismos alumnos se percaten de las dificultades de este método con ciertos polígonos.

Pida a una pareja de alumnos que elabore un cartel con esta información. Pregunte al grupo cómo podría haberse elaborado la tarjeta que hicieron al inicio de la sesión, utilizando la medida del ángulo central. Posteriormente puede solicitar a los alumnos que copien la información del recuadro en sus cuadernos. Otra forma de recuperar la información es pedirles que expliquen la técnica para trazar un polígono regular a partir del ángulo central, describiendo e ilustrando en su cuaderno cada uno de los pasos.