Propósito de la sesión. Construir polígonos regulares a partir de la medida de su lado y su ángulo interior. Organización del grupo. Se sugiere que los alumnos trabajen en parejas, a excepción de la actividad V de Manos a la obra, la cual puede resolverse individualmente. Materiales. Juego de geometría.

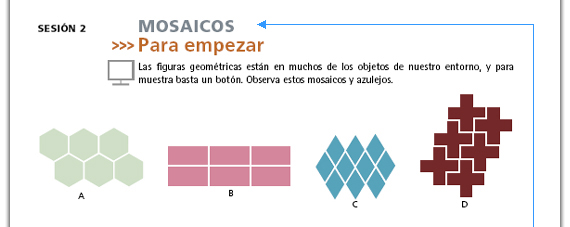
Respuestas: Sólo en el mosaico A hay polígonos regulares (hexágonos). Sugerencia didáctica. Invite a los alumnos a que argumenten sus respuestas; de ser necesario, recuérdeles las dos condiciones que determinan a un polígono regular: igualdad de lados e igualdad de ángulos.

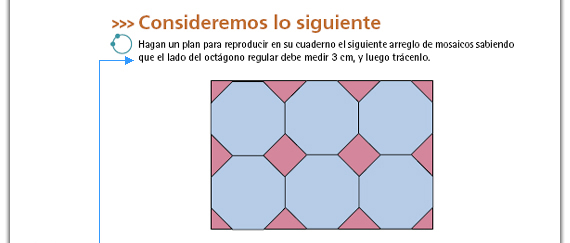
Propósito de la actividad. A diferencia del problema de la sesión anterior, en éste se pide que el octágono tenga cierta medida por lado, por lo que el procedimiento del ángulo central no es adecuado, ya que no se sabe la medida del radio de la circunferencia. A partir de esta nuevas condiciones se espera que los alumnos busquen otro procedimiento.

Posibles procedimientos. -Trazar una cuadrícula a partir de las esquinas de los cuadrados para formar los octágonos: El problema será determinar la medida de los cuadrados para que los octágonos salgan con todos los lados de 3 cm, además de determinar la inclinación de las líneas que cortarán los vértices del cuadrado. -Dado que el lado de cada hexágono mide 1 cm, reproducir la figura haciendo una ampliación a 3 cm, lo cual puede hacerse dibujando primero el rectángulo que comprende todo el mosaico y luego midiendo para encontrar los puntos que serán los vértices de los octágonos. -Trazar octágonos con el procedimiento usado en la sesión 1, aunque es muy difícil determinar la medida del radio de la circunferencia que debe trazarse; no obstante, podrían encontrar dicha circunferencia por ensayo y error trazando varios círculos y dividiéndolos en 8 partes, hasta obtener un octágono de 3 cm por lado. Se espera que algunos alumnos se den cuenta de la necesidad de medir los ángulos del octágono y que, a partir de trazar un lado de 3 cm, pueden trazar ángulos de 135º con lados de 3 cm, y formar así los octágonos pedidos. Si no terminan es importante que al menos intenten trazar un octágono.

Sugerencia didáctica. Mientras los alumnos resuelven, puede hacerles las siguientes preguntas: ¿Todos los ángulos interiores de un polígono regular son iguales? Si tenemos dos polígonos regulares de diferente tamaño pero de igual número de lados ¿sus ángulos interiores medirán lo mismo? Si nota que tienen dificultades para obtener la medida exacta de algunos ángulos (como en el caso del pentágono), sugiérales que den una medida aproximada, pues más adelante tendrán oportunidad de precisar las medidas.

Recuerde que. Si en un polígono regular se suma: la medida de su ángulo interior + la medida de su ángulo central, el resultado siempre es 180°.

Los ángulos que suman 180° se llaman suplementarios; por ejemplo, son parejas de ángulos suplementarios: 20° y 160° 45° y 135° 60° y 120° 72° y 108°

En un polígono regular el ángulo central es suplementario al ángulo interior.

Dado que un ángulo de 180° se llama llano o colineal lo anterior puede enunciarse como: el ángulo central y el ángulo interior de un polígono regular forman juntos un ángulo colineal.

Propósito de las actividades II y III. Que los alumnos descubran que el ángulo interior y el central de un polígono regular son suplementarios; esto les permitirá calcular algunos datos a partir de otros conocidos. En la sesión anterior los alumnos aprendieron a calcular el ángulo central conociendo el número de lados del polígono, esto implica que: -Pueden calcular el ángulo interior conociendo la medida del ángulo central o el número de lados. Por ejemplo, en el inciso c sabemos que un decágono tiene 10 lados, por lo que el ángulo central mide 36° (360 ÷ 10 = 36). Entonces el ángulo interior mide 144° porque 180 – 36 = 144 -Pueden calcular el número de lados conociendo la medida del ángulo central o del ángulo interior. Por ejemplo, en el inciso b sabemos que el ángulo interior mide 140°, entonces el ángulo central mide 40 porque 140 + 40 = 180; por lo tanto, la figura tiene 9 lados (9 x 40° = 360°)

Procure que los alumnos traten de leer e interpretar las instrucciones por sí mismos. De ser necesario, una vez que los alumnos hayan seguido el procedimiento de manera individual, invite a uno o a varios alumnos a mostrar en el pizarrón el procedimiento indicado.

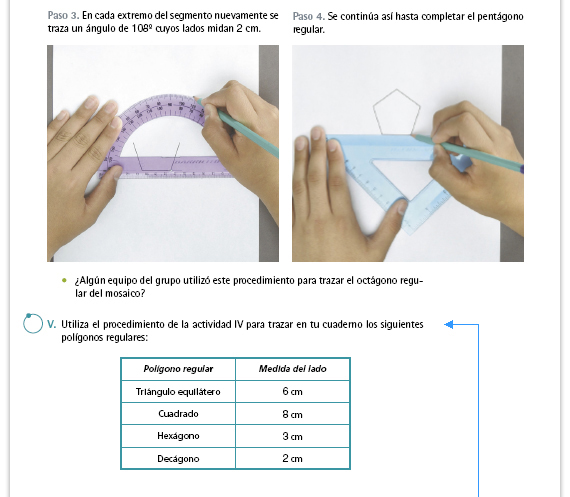
Propósito de la actividad. Que los alumnos practiquen el manejo de ciertas técnicas. Si lo cree necesario, usted puede sugerir otros ejercicios adicionales. Posibles dificultades. Algunos alumnos podrían tener problemas para decidir hacia qué dirección marcar el ángulo cada vez que deben trazarlo en el extremo de un segmento. Usted podría advertir a los alumnos de esta dificultad trazando una de las figuras en el pizarrón y preguntando en cada caso hacia dónde debe trazar cada uno de los ángulos, y ocasionalmente hacerlo de manera errónea para que los mismos alumnos se percaten y comenten esa dificultad.

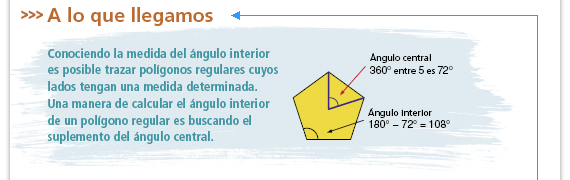
Una vez que lean y comenten lo enunciado puede solicitar a los alumnos que den otros ejemplos diferentes al del pentágono. Es importante señalar que, al igual que con los ángulos centrales, esta técnica únicamente funciona para polígonos regulares cuyo número de lados es un divisor de 360. Subraye con los alumnos que el dato de número de lados es esencial para el trazo: permite obtener la medida del ángulo central y, como consecuencia, la del ángulo interior. Otra forma de recuperar la información del recuadro es pedirles que escriban en el cuaderno las ideas fundamentales con sus propias palabras y que den otros ejemplos. Algunos de esos textos pueden leerse a todo el grupo.