Propósito de la sesión. Construir polígonos regulares a partir de informaciones como: ejes de simetría, ángulos centrales, ángulos interiores, etcétera. Organización del grupo: Se sugiere resolver todas las actividades en equipo. Materiales. Juego de geométría y colores.

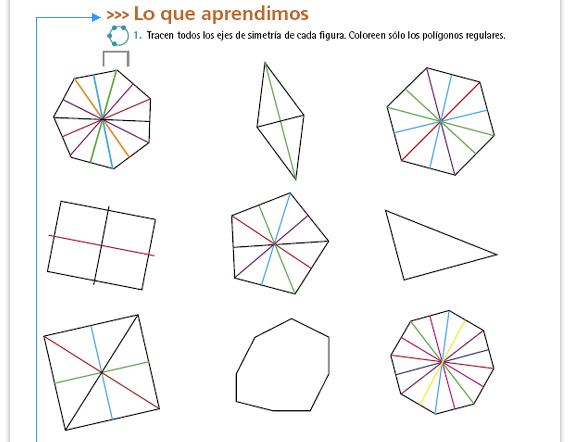
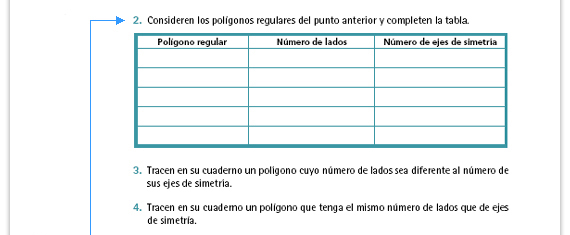
Propósito de las actividades. Las actividades 1 a 4 pretenden que los alumnos exploren otra propiedad interesante de los polígonos regulares: el número de lados y el número de ejes de simetría es el mismo. Por ello, en la actividad 3 los alumnos tendrán que trazar un polígono que no es regular (un rombo, un rectángulo o un triángulo isósceles, por ejemplo) y en la 4 uno que sí lo es. Se espera que al explorar sus trazos los mismos alumnos se den cuenta de esa diferencia, pero de todos modos es importante que usted lo comente durante la comparación de resultados. Respuesta 2. El número de lados debe coincidir con el número de ejes de simetría. Respuesta 3: Un rombo o un rectángulo, ya que son las figuras que tienen en los ejemplos. También puede ser un triángulo isósceles, o cualquier figura con varios lados que no sea regular (si no tiene ejes de simetría, entonces tiene más lados que ejes). Respuesta 4. Puede ser cualquier polígono regular.

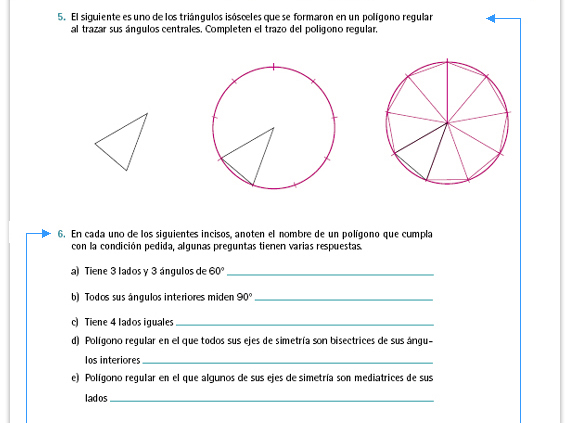
Sugerencia didáctica. Si el tiempo se lo permite puede seguir explorando la simetría de los polígonos regulares; en particular, puede mostrar cómo la simetría ayuda en el trazo de algunos polígonos. Por ejemplo, en primaria los alumnos aprendieron que al trazar un cuadrado en una circunferencia y trazar sus cuatro ejes prolongándolos para que corten a la circunferencia, pueden trazar un octágono; lo mismo pasa para el triángulo equilátero y el hexágono. En los ejercicios 6 y 7 los alumnos recordarán este trazo. También pueden trazar sólo la mitad de un polígono regular y a partir del eje de simetría pueden encontrar los puntos simétricos para terminar el polígono.

Respuestas. a) Triángulo equilátero. b) No se da la condición de que los polígonos sean regulares, por lo que puede ser cuadrado o rectángulo. c) No se da la condición de que los polígonos sean regulares, por lo que puede ser cuadrado o rombo. d) Pentágono, triángulo equilátero, heptágono, eneágono; en general, cualquier polígono regular con un número impar de lados. e) Cuadrado, hexágono, octágono, decágono; en general, cualquier polígono regular con un número par de lados.

Incorporar al portafolios. Los alumnos podrán completar el polígono regular atendiendo a diferentes relaciones: -Trazar una circunferencia con centro en el vértice donde se cortan los lados iguales del triángulo, tomando como radio precisamente, la medida de estos lados. En esa circunferencia trazarán el polígono al abrir el compás a la medida del lado desigual y marcando esa medida las veces que sea necesario alrededor de la circunferencia. -Medir el ángulo central y repetirlo las veces que sea necesario, para después trazar la circunferencia. -Medir los ángulos de la base del triángulo isósceles y a partir de esta medida calcular el ángulo interior del polígono regular y trazarlo a partir de ese dato. El ángulo central mide 40°, los ángulos interiores miden 140°; por lo tanto se trata de un eneágono regular (9 lados). Posibles dificultades. Si los alumnos no pueden resolver el problema o muestran ciertas dificultades en el trazo, repase con ellos los dos procedimientos que se trabajaron en esta secuencia para el trazo de polígonos regulares: a partir del ángulo central (actividades VI y V del Manos a la Obra, sesión 1) y a partir de los ángulos interiores (II y III).

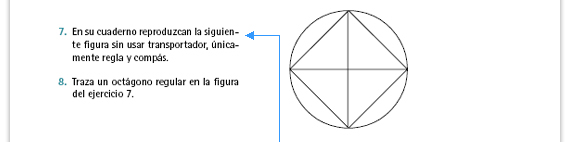
Posibles procedimientos. Una forma de resolverlo es trazar la circunferencia abriendo el compás según la medida del radio; dividir la circunferencia en cuatro partes trazando dos líneas perpendiculares que se cruzan en el centro de la circunferencia; unir los puntos en los que esas líneas cortan la circunferencia.

Posibles procedimientos. Una forma de resolver es trazando la figura anterior para, posteriormente, trazar las dos mediatrices de los lados del cuadrado. De esta forma la circunferencia queda dividida en 8 partes iguales.