Propósito de la sesión. Justificar las fórmulas para calcular el área del romboide y del rombo. Organización del grupo: Se recomienda que el problema inicial se resuelva en equipos, y la sección Manos a la obra en parejas. Materiales. Juego de geometría, hojas o papel para recortar y tijeras.

Propósito de la actividad. Debido a que las fórmulas que se trabajarán toman como referencia el área del rectángulo, esta actividad pretende que los alumnos recuerden la fórmula para calcular el área de esa figura (la han estudiado desde cuarto grado de primaria).

Posibles respuestas. Para el cuadrado: lado por lado, a × a. Para el rectángulo: base por altura, x por y.

Sugerencia didáctica. No obstante que en primaria los alumnos estudiaron el área de estas figuras, es probable que no recuerden las fórmulas, pero cuentan con otras herramientas. Anímelos a que traten de resolver el problema sin decirles, en este momento, cómo hacerlo.

Eje

Forma, espacio y medida.

Tema

Medida.

Antecedentes

Durante la escuela primaria los alumnos trabajaron con fórmulas para el cálculo de áreas y perímetros de algunas figuras; en este grado se pretende que aprendan a reconstruir y a justificar fórmulas empleando distintos recursos. Algunos de los conocimientos que los alumnos ya estudiaron y que sirven como apoyo para la resolución de estas situaciones, son: identificación y trazo de figuras geométricas (triángulos, rectángulos, cuadrados, rombos, romboides, trapecios y polígonos regulares) y cálculo de áreas mediante distintos procedimientos.

Propósitos de la secuencia Justificar las fórmulas para calcular el perímetro y el área de triángulos, cuadriláteros y polígonos regulares.
Sesión	Título y propósitos de la sesión	Recursos
1	Rompecabezas 1 Justificar las fórmulas para calcular el área del romboide y del rombo.	Video "¿Dónde se utilizan las fracciones?" Interactivo
2	Rompecabezas 2 Justificar las fórmulas para calcular el área del triángulo y del trapecio.	Interactivo
3	Descomposición de figuras Justificar las fórmulas para calcular el área de polígonos regulares.	Video "El sistema solar y la fuerza de gravedad" Interactivo
4	Otras formas de justificar las fórmulas Conocer otras formas de justificar las fórmulas estudiadas en las sesiones anteriores y justificar algunas fórmulas de perímetros.	Interactivo Video "Justificación"

Propósito de la actividad. Las figuras no tienen las medidas indicadas porque es importante que los alumnos aprendan a tomar la decisión de qué medidas deben considerar y cómo deben hacerlo (por ejemplo, cómo medir la altura de un romboide). En el caso del romboide son necesarias las medidas de la base y de la altura; en el rombo se requieren las medidas de las diagonales. Aun si se parten las figuras en triángulos, se necesitan estas medidas, aunque es posible que algunos alumnos las tomen por partes. Posibles procedimientos. Descomponer cada figura en otras de las que ya conocen la fórmula. Por ejemplo, el romboide puede descomponerse en un rectángulo y dos triángulos; posteriormente se calcula el área de los triángulos y los rectángulos y se suman. Reproducir las figuras en una hoja y hacerles cortes para que, a manera de rompecabezas, armen alguna figura de la que ya saben calcular el área, como el rectángulo (los alumnos han trabajado con rompecabezas desde primer grado de primaria). Como en la primaria han calculado áreas cuadriculando la figura es probable que algunos opten por este procedimiento, aunque deberán tener cuidado de que cada cuadrito sea de 1 cm2. Usando la fórmula correspondiente. Este es un procedimiento que los alumnos pueden seguir si es que recuerdan dichas fórmulas y saben usarlas. Respuesta. El romboide tiene 18 cm2 y el rombo 12 cm2.

Propósito de la actividad. Que los alumnos se den cuenta de que cualquier romboide puede transformarse en un rectángulo con las mismas medidas para la base y la altura, de ahí que la fórmula para calcular el área del romboide es la misma para calcular el área del rectángulo: el producto de la base por la altura. Respuesta: Una forma de resolverlo es trazar las alturas del romboide que pasan por los vértices contrarios formando triángulos; se recorta uno de esos triángulos y se cambia de lugar para obtener el rectángulo.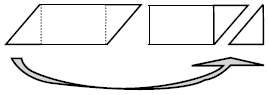

Respuestas (incisos b, c, d). Las medidas de la base del rectángulo y del romboide son iguales; las medidas de la altura del rectángulo y del romboide son iguales; y las áreas del romboide y del rectángulo son iguales. Todas estas relaciones pueden constatarse al rearmar el romboide sobre el rectángulo.

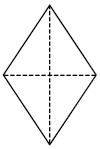
Propósito de la actividad. Que los alumnos, a través de la manipulación de la figura, se den cuenta de que el rombo puede transformarse en un rectángulo cuya base es igual a una de las diagonales, y su altura es igual a la mitad de la otra diagonal. A partir de ahí podrán justificar la fórmula para calcular el área del rombo. Respuesta. Una forma de obtener el rectángulo a partir del rombo es la siguiente: se trazan las diagonales del rombo y se corta a través de ellas para obtener 4 triángulos iguales; con ellos se arma el rectángulo.

Respuestas (incisos b y c). La base del rectángulo y la medida de la diagonal menor del rombo son iguales. El área del rombo y el área del rectángulo son iguales. Lo anterior puede constatarse al rearmar el rombo sobre el rectángulo.

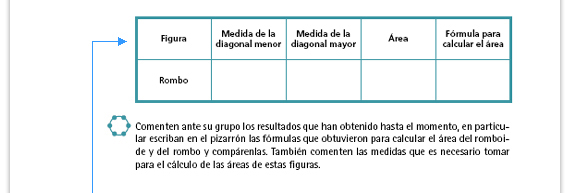
Respuesta. La fórmula es diagonal menor por diagonal mayor, entre dos. O cualquiera de sus expresiones equivalentes.

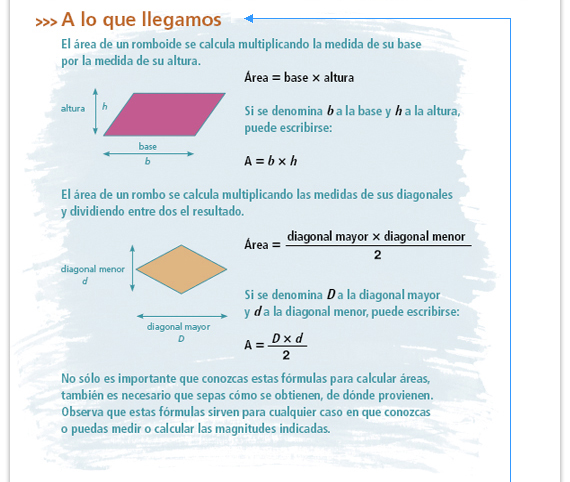
En este apartado se formalizan los hallazgos que los alumnos han experimentado durante toda la sesión. Se espera que a partir de esa experiencia puedan comprender lo enunciado. Sugerencia didáctica. Es importante que en el transcurso de la lectura usted y los alumnos hagan comentarios respecto de cómo se obtienen estas fórmulas. Recuerde que la práctica cotidiana de la argumentación verbal ayuda a los alumnos a desarrollar gradualmente un pensamiento deductivo, lo que les permitirá además desarrollar la habilidad para justificar sus respuestas y para hacer demostraciones sencillas de sus argumentos. Los alumnos pueden registrar en sus cuadernos no sólo las fórmulas sino también una pequeña explicación que pueden ilustrar con figuras de papel o con dibujos.