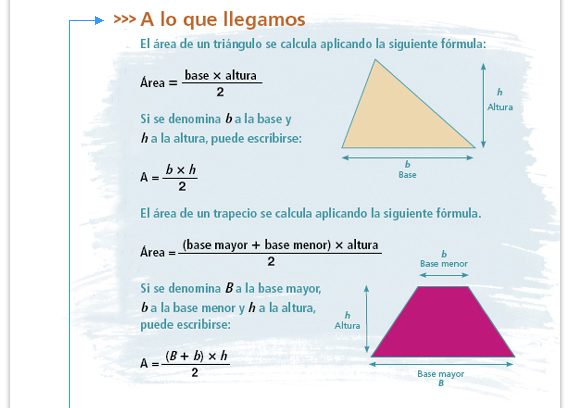
Propósito de la sesión. Justificar las fórmulas para calcular el área del triángulo y del trapecio. Organización del grupo. Forme equipos para que resuelvan el problema inicial; posteriormente organice parejas para trabajar el resto de la sesión. Materiales. Juego de geometría y tijeras.

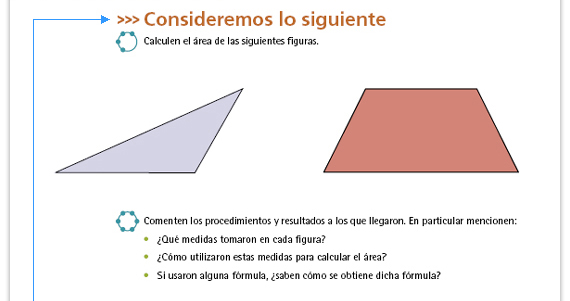
Sugerencia didáctica. Mientras los alumnos resuelven, usted puede observar el trabajo de los equipos para identificar sus procedimientos de resolución y sus dificultades. Anime a los equipos a que comenten y decidan cuáles son las medidas que deben tomar en cuenta para calcular el área de cada figura. Posibles procedimientos. Descomponer las figuras en otras conocidas. Por ejemplo, recortar las piezas y formar con ellas las figuras conocidas. En el caso del triángulo, es posible que algunos equipos completen la figura para obtener un triángulo rectángulo. Cuadricular cada figura y contar el total de unidades cuadradas. Usar las fórmulas (quienes las recuerden), aunque en el caso del triángulo algunos alumnos podrían tener dificultades para identificar la altura. Respuesta. Área del triángulo, 7.5 cm2, y área del trapecio, 16.5 cm2

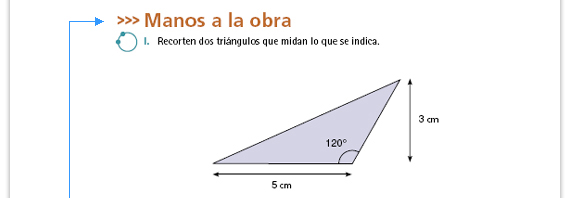
Sugerencia didáctica. Lo importante de la actividad I es que los alumnos deduzcan la fórmula del triángulo, por lo que usted puede auxiliarlos en el trazo de la figura indicándoles cómo hacerlo. Incluso, si nota que varias parejas tienen problemas, los trazos pueden hacerse de manera grupal para que después cada pareja resuelva los siguientes incisos.

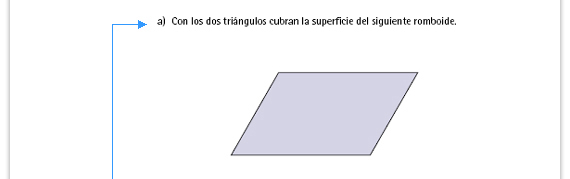
Propósito de la actividad. Se espera que los alumnos deduzcan que dos triángulos iguales siempre forman un romboide (o un rectángulo) y que por lo tanto su área se calcula multiplicando base por altura y dividiendo el resultado a la mitad.

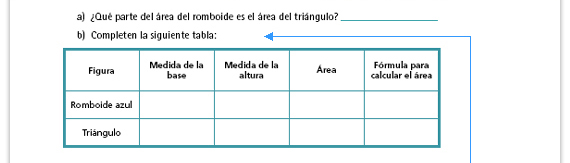
Propósito de la actividad. Que a partir del cálculo del área del romboide los alumnos identifiquen la relación entre las dimensiones y áreas del triángulo y del romboide, de tal manera que puedan establecer, para cada una de las figuras, una fórmula que les permita calcular su área. Es posible que algunas de las fórmulas que los alumnos propongan sean incorrectas; podrán regresar a ellas y corregirlas al final de este apartado. Respuesta. Para el romboide, b × h; para el triángulo b × h (y todas las fórmulas equivalentes a cada una de las anteriores).

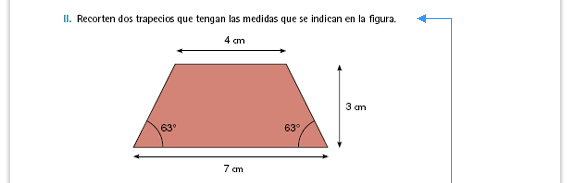
Sugerencia didáctica. También en este caso puede indicar al grupo cómo trazar la figura, para agilizar el desarrollo de las otras actividades.

Propósito de la actividad. Que los alumnos se den cuenta de que a partir de dos trapecios iguales siempre es posible formar un romboide (o un rectángulo) cuya base es igual a la suma de las bases del trapecio y cuya altura es igual a la altura del trapecio. A partir de lo anterior, los alumnos podrán deducir la fórmula para calcular el área del trapecio.

Respuestas. b) La base del romboide es la suma de la base mayor y la base menor del trapecio. c) La mitad. d) Base mayor más base menor por altura entre dos (y otras expresiones equivalentes).

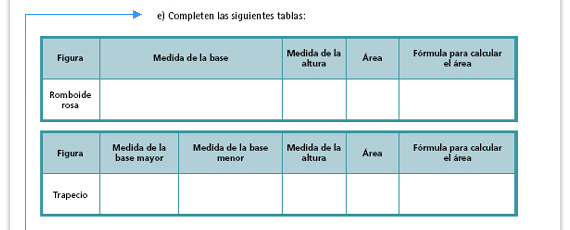
Propósito de la actividad. Que a partir del cálculo del área del romboide los alumnos identifiquen las relaciones entre las dimensiones y áreas del romboide y del trapecio, de tal manera que puedan establecer una fórmula que les permita calcular el área del trapecio. Es posible que algunas de las fórmulas que los alumnos propongan sean incorrectas; podrán regresar a ellas y corregirlas con la información de A lo que llegamos.

Sugerencia didáctica. Durante la confrontación de resultados ponga especial cuidado en los argumentos que los alumnos den para justificar las fórmulas de áreas. Recuerde que generalmente los alumnos saben más de lo que pueden expresar, por lo que es importante desarrollar en ellos su habilidad para argumentar y justificar sus ideas.

Pida a los alumnos que escriban en su cuaderno las fórmulas para obtener el área de cada una de las figuras y que redacten un texto breve en el que expliquen (justifiquen) por qué esas fórmulas permiten obtener el área. Invite a los alumnos a ilustrar en sus cuadernos, ya sea con dibujos o con el pegado de figuras, sus explicaciones.