Propósito de la sesión. Conocer otras formas de justificar las fórmulas estudiadas en las sesiones anteriores y justificar algunas fórmulas de perímetros. Organización del grupo. Se sugiere formar equipos para que trabajen de esa manera durante toda la sesión. Materiales. Juego de geometría y tijeras.

Propósito de las actividades 1y 2. Se espera que, a partir de las experiencias y conocimientos adquiridos en las sesiones anteriores, los alumnos realicen transformaciones de figuras que permiten justificar, de una manera distinta, las fórmulas que ya estudiaron. Asimismo, que sean capaces de elaborar argumentos que justifiquen esas fórmulas. Sugerencia didáctica. Aun cuando haya alumnos que puedan deducir y justificar las fórmulas a partir de los dibujos, invítelos a que tracen, recorten y transformen las figuras como se indica, lo cual contribuye al desarrollo de su percepción geométrica y de su imaginación espacial; particularmente este tipo de actividades es un apoyo para aquellos estudiantes que aún necesitan un referente concreto.

Posibles respuestas. El triángulo se transformó en un rectángulo con la misma altura y con base igual a la mitad de la base del triángulo. Dado que el área del rectángulo se obtiene multiplicando base por altura, tenemos que el área del triángulo se obtiene multiplicando base por altura entre dos. Posibles dificultades. Es muy probable que las justificaciones que den los alumnos: Sean erróneas o contengan implicaciones falsas. Estén mal redactas, no sigan una secuencia lógica adecuada o que sean incomprensibles.

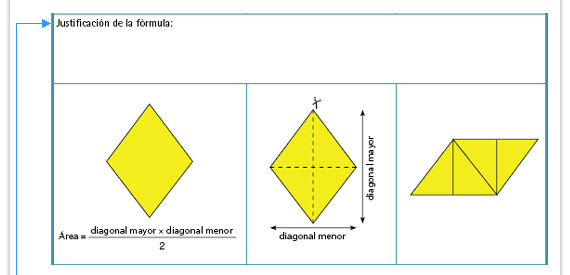
Posible respuesta. El rombo se transformó en un romboide en el que la base es la diagonal menor y la altura es la mitad de la diagonal mayor. Por ello para obtener el área, se multiplica diagonal mayor por diagonal menor, y luego se divide entre dos. Justificar es una habilidad difícil de desarrollar, lo que no se logra en una sola sesión. Procure crear un ambiente de respeto durante la puesta en común para que los alumnos se sientan en confianza y lean sus justificaciones, aunque no sean del todo correctas. En caso de haber errores es importante que se aproveche el momento para corregirlos. Una estrategia es que una vez que todos los equipos lean sus justificaciones, se escojan las que consideren acertadas y se mejoren de manera grupal.

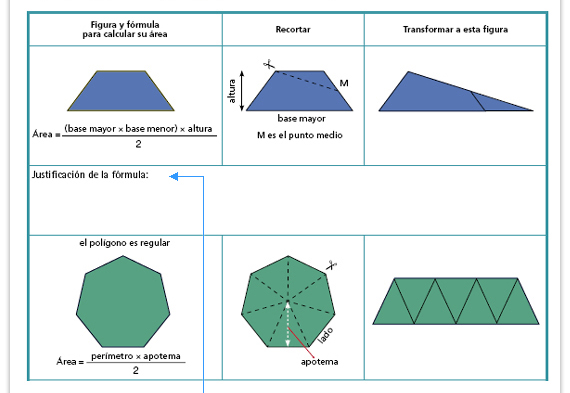
Posible respuesta. El trapecio se transformó en un triángulo con la misma altura y con base igual a la suma de las bases del trapecio. Por ello, la fórmula para calcular el área de un trapecio es base mayor más base menor, por altura, entre dos.

Posible respuesta. El polígono se transformó en un trapecio con altura igual a la apotema y en el que la suma de sus bases es igual al perímetro del polígono. Para calcular el área del trapecio sumamos base mayor más base menor, por la altura, entre dos; notamos que la base mayor más la base menor es el perímetro del polígono, y la altura es la apotema del polígono.

Posible respuesta. El rectángulo está formado por dos rombos iguales (uno de ellos se descompuso en triángulos). El rectángulo tiene como base la diagonal menor y como altura la diagonal mayor. Por eso, para calcular el área del rombo se multiplica la diagonal mayor por la diagonal menor; y como el área del rombo es la mitad del área del rectángulo, se divide después entre dos. Incorporar al portafolios. Si los alumnos tienen dificultades para justificar la fórmula revise junto con ellos las actividades número II del apartado Manos a la obra de la sesión 1. A partir de las transformaciones del rombo en rectángulo, ayude a los alumnos a establecer relaciones entre estas dos figuras (las preguntas y las tablas de esa sección están dirigidas al establecimiento de tales relaciones).

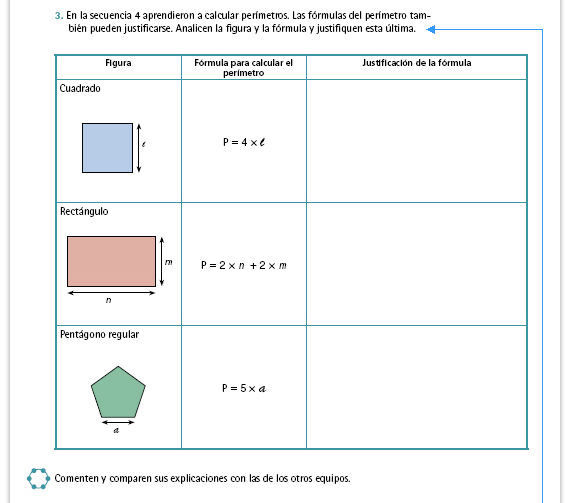
Propósito de la actividad. Si bien el programa indica que los alumnos deben justificar fórmulas de áreas y perímetros, habrá notado que la mayoría de las actividades se centran en el área. La razón es que en el caso del perímetro es suficiente comprender el concepto de "perímetro" y conocer las magnitudes de la figura para justificar las fórmulas del mismo; por ello sólo se ha dedicado esta actividad para abordar ese aspecto.

Propósito del video. Observar ejemplos gráficos en los que se justifican algunas fórmulas de área o perímetro de polígonos.