Propósito de la sesión. Resolver problemas de cantidades directamente proporcionales en contexto de escalas mediante el uso de la constante de proporcionalidad. Organización del grupo. La sesión se trabaja en parejas.

Eje

Manejo de la información.

Tema

Análisis de la información.

Antecedentes

En el bloque 1 los alumnos identificaron y resolvieron problemas de proporcionalidad directa del tipo "valor faltante"; para ello utilizaron distintos procedimientos de solución, particularmente el cálculo del valor unitario. En esta secuencia los alumnos continuarán identificando y resolviendo ese tipo de situaciones y se espera que sean capaces de utilizar procedimientos expertos.

Propósitos de la secuencia Identificar y resolver situaciones de proporcionalidad directa del tipo "valor faltante" en diversos contextos, utilizando procedimientos expertos.
Sesión	Título y propósitos de la sesión	Recursos
1	La cancha de básquetbol Resolver problemas de cantidades directamente proporcionales en contexto de escalas mediante el uso de la constante de proporcionalidad.	Interactivo
2	Mapas y escalas Resolver problemas de cantidades directamente proporcionales en contexto de escalas en los que la constante de proporcionalidad es una fracción unitaria.	Video "Centro Histórico de la Ciudad de México"
3	Descomposición de figuras Justificar las fórmulas para calcular el área de polígonos regulares.

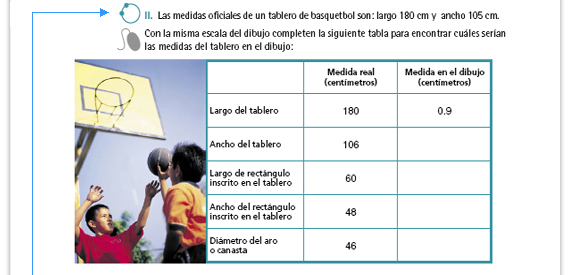
Respuestas. Cada medida en el dibujo debe multiplicarse por 100 para obtener la medida real, o bien, dividir entre 100 la medida real para obtener la del dibujo.

Posibles procedimientos. La multiplicación y la división por potencias de 10 son operaciones que pueden resolverse de distintas maneras. Los alumnos pueden resolverlas por escrito o de formas más económicas, como calculando mentalmente, o bien, recorriendo el punto decimal o aumentando ceros. Aprender reglas o técnicas para el cálculo es muy útil, sin embargo, también es importante saber por qué funcionan. Si los alumnos las utilizan pregúnteles si saben por qué da lo mismo recorrer el punto que hacer la multiplicación, por ejemplo.

Sugerencia didáctica. Estos conceptos serán de mucha importancia en la secundaria, ya que se irán ampliando y vinculando con otros y darán paso a diversos aprendizajes (como la función lineal). Comente con los alumnos que el factor de escala es lo mismo que la constante de proporcionalidad, pero el factor de escala: -Se utiliza en situaciones que involucran mapas, planos, croquis y otras representaciones geográficas. -Involucra cantidades de la misma magnitud (por ejemplo, "centímetros" a "centímetros", que son unidades de longitud; no del tipo "caramelos" a "dinero"). -Da información de cuántas veces más grande es una medida real que su representación en el dibujo. También puede ser útil recordar el concepto de valor unitario y comentar cómo se relaciona con el factor de escala o constante de proporcionalidad. En una situación de proporcionalidad directa se relacionan dos magnitudes (como dinero y caramelos) o dos valores de una misma magnitud (como centímetros con centímetros o centímetros con metros). El valor unitario es el valor de una de las magnitudes cuando el valor de la otra es 1. Por ejemplo, si tres caramelos cuestan $6, un caramelo cuesta $2. El valor unitario es 2 pesos y la constante de proporcionalidad es 2 pesos por cada caramelo. Dos es el número que permite encontrar el costo de cualquier cantidad de caramelos. Por ejemplo, si queremos saber cuánto cuestan 3 caramelos basta multiplicar 3 × 2 = 6, así que 3 caramelos cuestan 6 pesos.

Propósito del interactivo. Resolver problemas de proporcionalidad directa.

Respuestas. a) A cada centímetro en la medida real corresponde 0.01cm en el dibujo. Así, 0.01 centímetros es el valor unitario que nos permite pasar de las medidas reales del tablero para obtener su medida en el dibujo. b) Por 0.01 Posibles dificultades. Es posible que algunos alumnos digan que el valor unitario es 100 porque para obtener las medidas del dibujo, las medidas reales deben dividirse entre 100. Aunque esto es correcto, se refiere más a la operación que hay que hacer para llenar la tabla y no a lo que significa el valor unitario. El valor unitario es aquel que permite saber a cuánto equivale 1 cm de la medida real en el dibujo, y la respuesta es 0.01 cm

Sugerencia didáctica. Comente con los alumnos que, efectivamente, 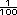o 0.01 es la constante de proporcionalidad o factor de escala, pero que tambien es el valor unitario, porque a cada centímetro de las medidas reales corresponde 0.01 centímetros en el dibujo.

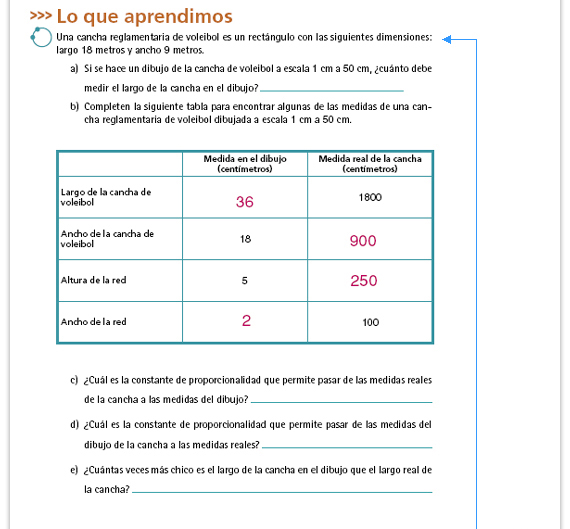
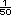Integrar al portafolios. Pida a los alumnos que le entreguen las respuestas a las preguntas c, d y f. Si no son correctas, revise nuevamente esta sesión. Respuestas. a) El largo de la cancha es de 18 m o 1 800 cm. Según el factor de escala, 50 cm de la cancha medirán 1 cm en el dibujo, así que se divide 1 800 entre 50 y resulta 36. El largo de la cancha en el dibujo medirá 36 cm. c) Es (porque para obtener las medidas del dibujo cada medida real se multiplica por ). d) 50, porque cada medida en el dibujo se multiplica por 50. e) Es 50 veces más chico.