
|

|

|
 |
 |

| Propósitos de la sesión. Resolver
problemas de cantidades directamente
proporcionales identificando la
aplicación inversa de la constante de
proporcionalidad.
Utilizar los procedimientos aprendidos durante la secuencia para resolver situaciones de proporcionalidad directa en diversos contextos. Organización del grupo. Se sugiere trabajar la sesión en parejas, excepto la sección Lo que aprendimos y cuando haya momentos de discusión grupal. |

| Sugerencia didáctica. Antes de que las parejas empiecen a resolver es recomendable que abra un espacio para que los alumnos comenten de qué se trata el problema. |

| Propósito de la actividad. En este
problema es importante que los
alumnos lleguen a establecer que
el rendimiento de un camión es el
número de kilómetros que recorre por
cada litro de gasolina (km/l). Permita
que lo resuelvan con sus propios
procedimientos y en este momento
no intervenga. Más adelante podrán
comentarlos, detectar dudas y corregir
errores.
Respuestas.
|
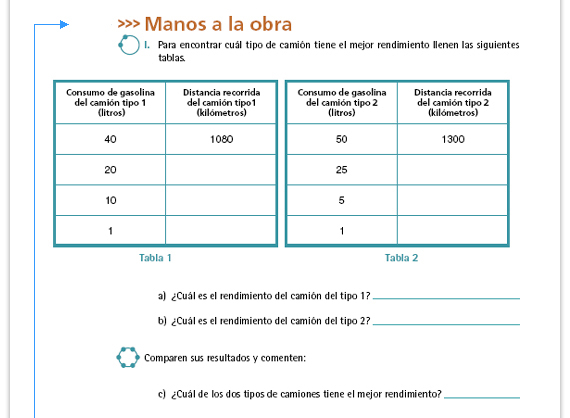
| Propósito de la actividad. Las tablas pretenden apoyar a los alumnos para que obtengan el valor unitario mediante el cálculo de otros valores. |
| Cuando las hayan completado invítelos a comparar sus respuestas con las que obtuvieron en la sección Consideremos lo siguiente. |

Respuestas.
Para el camion tipo 1.
1 km recorrido: 1 entre 27 = 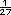 litros o
0.037037... litros (como es un decimal
periódico puede sugerirles que lo
trunquen o lo redondeen). litros o
0.037037... litros (como es un decimal
periódico puede sugerirles que lo
trunquen o lo redondeen). |
682 km recorridos: 682 entre 27 = 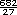 = 25
= 25 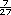 o 25.26 litros (redondeando). o 25.26 litros (redondeando). |
Para el camión tipo 2.
1 km recorrido: 1 entre 26 = 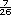 o
0.038 litros (redondeando). o
0.038 litros (redondeando). |
682 km recorridos:
682 entre 26 = 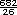 = 26 = 26 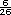 o 26.23
litros (redondeando). o 26.23
litros (redondeando). |
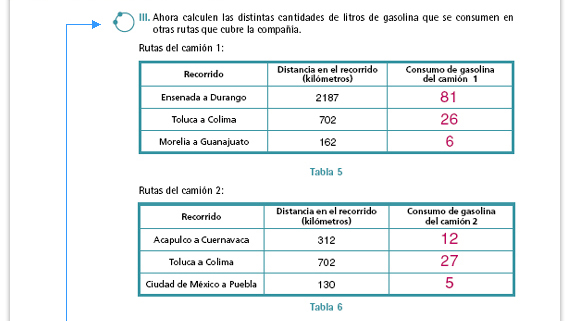
| Propósito de la actividad. Se
pretende que los alumnos hagan uso
de la constante de proporcionalidad,
identificándola como el número que
permite pasar de la distancia recorrida
al consumo de gasolina.
Respuestas. Para conocer cuál es el consumo de gasolina se divide el número de kilómetros de cada recorrido entre la constante de proporcionalidad. |

Respuestas. Sabemos que el camión
1 tiene un rendimiento de 27 km por
cada litro de gasolina. Para saber
cuantos litros de gasolina gasta en
un recorrido de 162 km se divide 162
entre 27, o bien, se multiplica 162 por
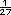 . La constante de proporcionalidad
en la tabla 5 es . La constante de proporcionalidad
en la tabla 5 es 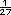 (porque se
multiplica por (porque se
multiplica por 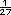 o se divide entre 27).
En la tabla 6 es o se divide entre 27).
En la tabla 6 es 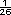 |
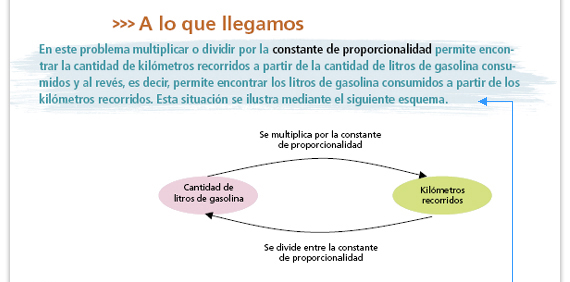
 Sugerencia didáctica. La finalidad
de la información que se presenta
en este apartado es que los alumnos
establezcan la acción inversa de la
constante de proporcionalidad.
Además de comentar esta información
con el grupo, pida a los alumnos
que busquen en la misma secuencia
ejemplos que ilustren la aplicación de
estas dos constantes.
Sugerencia didáctica. La finalidad
de la información que se presenta
en este apartado es que los alumnos
establezcan la acción inversa de la
constante de proporcionalidad.
Además de comentar esta información
con el grupo, pida a los alumnos
que busquen en la misma secuencia
ejemplos que ilustren la aplicación de
estas dos constantes. |

Respuestas.
|

| Integrar al portafolios. Analice
las respuestas de los alumnos y si
es necesario revisen conjuntamente
la sección Manos a la obra de la
secuencia 1 y de la secuencia 3.
Respuestas.
|
 (se multiplica por
(se multiplica por  o por 1.6
o por 1.6
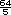 (12.8 cm), y el que media
11 cm debe medir
(12.8 cm), y el que media
11 cm debe medir 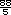 (17.6 cm).
(17.6 cm).
 ).
).