Propósito de la sesión. Resolver problemas de cantidades directamente proporcionales en los que se aplican sucesivamente dos factores constantes de proporcionalidad. Organización del grupo. La sesión se trabaja en parejas.

Propósito del video. Identificar problemas con cantidades directamente proporcionales en donde se aplican sucesivamente dos constantes de proporcionalidad.

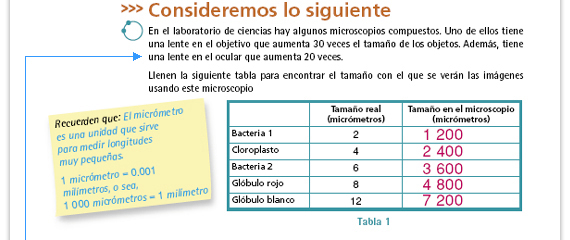
Propósito de la actividad. En esta situación se ponen en juego dos constantes de proporcionalidad que se aplican sucesivamente: × 30 (lente del objetivo) y × 20 (lente del ocular). Posibles dificultades. Probablemente algunos alumnos cometan errores como: -Sumar las constantes de proporcionalidad (30 + 20 = 50 como ampliación final). -Considerar sólo una de las constantes (ya sea x 20 o × 30) como la ampliación final. Mientras las parejas resuelven, usted puede observar qué procedimientos utilizan y cuáles son los errores más frecuentes, para que posteriormente pueda retomarlos y ponerlos a consideración del grupo.

Eje

Manejo de la información.

Tema

Análisis de la información.

Antecedentes

En la secuencia anterior los alumnos resolvieron problemas de proporcionalidad directa identificando la constante de proporcionalidad. En esta secuencia los alumnos aplicarán constantes de proporcionalidad de manera sucesiva.

Propósitos de la secuencia Interpretar el efecto de la aplicación sucesiva de factores constantes de proporcionalidad en situaciones dadas.
Sesión	Título y propósitos de la sesión	Recursos	Vínculos
1	Microscopios compuestos Resolver problemas de cantidades directamente proporcionales en los que se aplican sucesivamente dos factores constantes de proporcionalidad.	Video "Microscopios compuestos" Interactivo
2	Escalas y reducciones Resolver problemas de cantidades directamente proporcionales en los que la constante de proporcionalidad es una fracción unitaria.	Interactivo
3	Consomé ranchero Resolver problemas de cantidades directamente proporcionales mediante la aplicación sucesiva de constantes de proporcionalidad.		Ciencias Secuencia 12

Sugerencia didáctica. Pida a dos o tres parejas que hayan obtenido resultados distintos entre sí que expliquen cómo los obtuvieron. No es necesario que en este momento se agote la discusión sobre cuáles resultados son correctos y cuáles no, pues en la siguiente parte de la sesión podrán verificar sus respuestas.

Propósito de la actividad. Se espera que los alumnos puedan contrastar los resultados que obtuvieron en la tabla 1 con las medidas que se establecen como correctas en la tabla 2. Las de las células vegetal y animal les permiten comparar de manera directa los resultados que obtuvieron para el glóbulo rojo y para el glóbulo blanco, pues las medidas originales son las mismas, respectivamente.

Sugerencia didáctica. Esta es una oportunidad para retomar la discusión de procedimientos y resultados que pudo haber quedado inconclusa en el problema inicial.

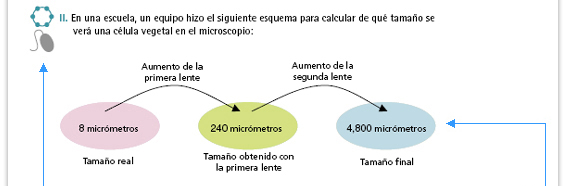
Propósito del interactivo. Ejemplificar la aplicación sucesiva de la constante de proporcionalidad.

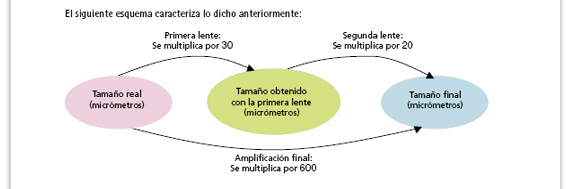
Sugerencia didáctica. El esquema muestra a los alumnos un procedimiento con el que pueden resolver este tipo de problemas, pues permite analizar las transformaciones que sucesivamente fue sufriendo el tamaño original al ser visto al través de cada una de las lentes. Analícelo con los alumnos.

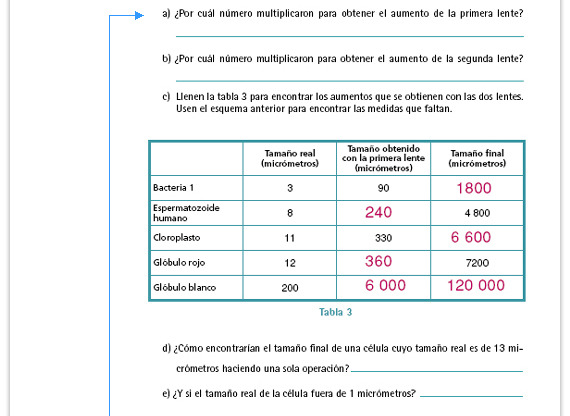
Respuestas a) La primera lente aumenta 30 veces las medidas originales, así que se obtiene una medida de 240 micras (8 × 30). b) Por 20 (porque 240 × 20 = 4 800) d) Multiplicando 13 × 600. Multiplicar por 30 y luego por 20 es lo mismo que multiplicar por 600 (30 × 20). e) 1 × 600.

Sugerencia didáctica. Pida a los alumnos que copien en sus cuadernos el esquema y que redacten un texto en el que expliquen, con sus propias palabras, cómo se obtiene la constante de proporcionalidad correspondiente a la amplificación final. También puede dejar como tarea el mismo problema, pero cambiando algunos datos, por ejemplo: ahora el aumento con la primera lente será de 15 veces y el de la segunda lente será de 45 veces. ¿Cuál será el aumento final?