Propósito de la sesión. Resolver problemas de cantidades directamente proporcionales en los que la constante de proporcionalidad es una fracción unitaria. Organización del grupo. La sesión se trabaja en parejas y en equipos.

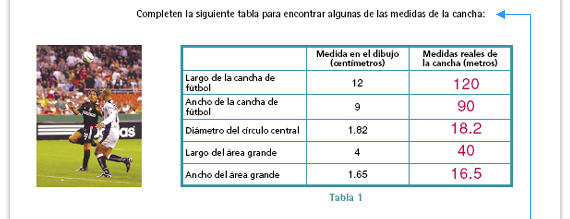
Propósito de la actividad. En esta actividad se pretende ver el paso de la medida del dibujo a la medida real como la aplicación de una constante de proporcionalidad, y ver a la conversión de metros a centímetros (para tener el valor del dibujo y el de la medida real en la misma unidad) como la aplicación de otra constante. Se espera que los alumnos hagan uso de procedimientos y recursos que ya han utilizado en situaciones similares: obtención del valor unitario y de la constante de proporcionalidad.

Respuestas. a) 10 b) 1 cm a 1 000 cm c) Es 1 000 veces más grande. Posibles dificultades. Algunos alumnos podrían responder que las medidas de la cancha son 10 veces más grandes con respecto a las del dibujo. Esa respuesta es incorrecta porque no está considerando el cambio de unidad (de centímetros a metros). No los corrija en este momento, permita que resuelvan la sección Manos a la obra.

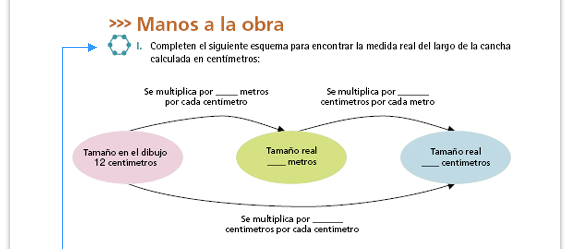
Sugerencia didáctica. El esquema representa el efecto de la aplicación sucesiva de dos constantes de proporcionalidad. Dibújelo en el pizarrón para completarlo y analizarlo junto con los alumnos. Enfatice que: -El esquema puede analizarse viendo las flechas de arriba. Se aplica una primera constante para pasar de la medida del dibujo en centímetros a la real en metros. La primera constante es 10 metros por cada centímetro. Después viene la aplicación de la segunda constante para pasar la medida real en metros a centímetros. Como cada metro tiene 100 centímetros, la segunda constante es 100 centímetros por cada metro. -También puede analizarse viéndolo por la flecha de abajo. Esa única flecha "compone" la aplicación de las dos constantes (10 y 100) en una sola. Por eso pasa de la medida del dibujo a la medida real en centímetros con una sola operación (por 1 000).

Sugerencia didáctica. Diga a los alumnos que comparen su respuesta a esta pregunta con la que dieron en el inciso c de la sección anterior. Si hay diferencias, pídales que expliquen por qué y hagan las correcciones pertinentes.

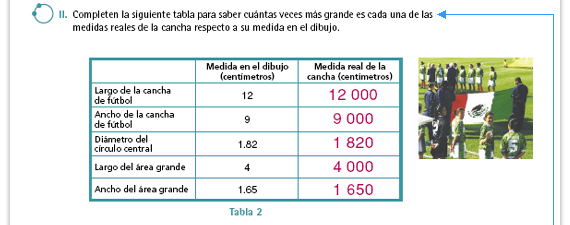
Respuestas. Se aplica a cada medida del dibujo la composición de las dos constantes de proporcionalidad, es decir, se multiplican por 1 000.

Respuestas. El factor de escala es 1 cm a 1 000 cm.

Sugerencia didáctica. Lea junto con los alumnos la información del recuadro y vayan señalando en el siguiente esquema cada una de las constantes que se mencionan. Cuando terminen puede preguntarles: ¿cómo se puede pasar de la medida del dibujo (en centímetros) a la medida real en centímetros haciendo una sola operación?

Propósito de la actividad. Ahora se pretende que los alumnos apliquen una constante de manera inversa, es decir, si ya se conoce la medida real en metros, hallar la medida en el dibujo (en centímetros).Sugerencia didáctica. Pida a los alumnos que hagan mentalmente las operaciones necesarias para llenar la tabla. Esto les ayudará a practicar el cálculo mental con divisiones entre 10. Pongan especial atención en la medida del ancho de los postes de la portería, porque hay que añadir un cero. Respuestas. Hay que dividir cada medida real entre 10 para obtener la del dibujo (o recorrer el punto un lugar hacia la izquierda).

Propósito del interactivo. Ejemplificar la aplicación sucesiva de la constante de proporcionalidad.

Respuestas. a) Es (se multiplica por o se divide entre 10). b) Son 1 000 veces más chicas.

Sugerencia didáctica. Pregunte a los alumnos como encontraron las medidas de la tabla 3: Alguien dividió entre 10?, alguien multiplicó por 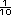?, Se obtiene el mismo resultado con ambos procedimientos?, Por qué?