|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas de cantidades directamente
proporcionales mediante la
aplicación sucesiva de constantes de
proporcionalidad.
Organización del grupo. Se propone resolver la sesión en parejas y en equipos. La sección Lo que aprendimos es individual. |

Propósito de la actividad. Se
aborda la aplicacion sucesiva de dos
constantes de proporcionalidad, una
que divide y otra que multiplica (en
este caso, dividir entre 5 y multiplicar
por 8). La operacion que permite
"componer" las dos constantes es
multiplicar por  . .
Posibles procedimientos. El problema puede ser resuelto de distintas maneras; una de ellas es que los alumnos intenten calcular la cantidad que se requiere de cada ingrediente para una porción (valor unitario). Una vez obtenida, se multiplica esa cantidad por 8 porciones. Otra forma de resolverlo es multiplicar por 8 las cantidades de cada uno de los ingredientes, y después dividir entre 5 cada una de ellas; el resultado que se obtiene es el mismo que con el procedimiento anterior. Es posible que algunos alumnos expresen los resultados con números decimales. Pídales que también lo hagan con fracciones. Posibles dificultades. Los alumnos podrían:
Esos dos procedimientos son incorrectos. No los corrija ahora, más adelante tendrán oportunidad de hacerlo. Respuestas. Todas las cantidades deben multiplicarse por 
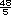 tazas de caldo de pollo. tazas de caldo de pollo.
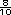 de pechuga. de pechuga.
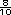 de cebolla. de cebolla.
 de jitomate picado. de jitomate picado.
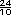 tazas de arroz cocido. tazas de arroz cocido.
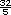 cucharadas de cilantro picado. cucharadas de cilantro picado.
|
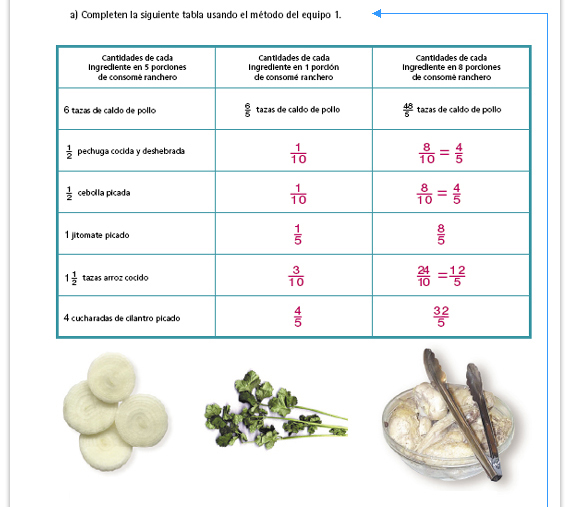
Propósito de la actividad. En esta
tabla se explicita la aplicacion de las
dos constantes: primero entre 5 y
despues por 8 (que es lo mismo que
multiplicar por  ). ).
Sugerencia didáctica. Antes de que las parejas empiecen a resolver, es conveniente que en el grupo se comente el procedimiento que se explica en el texto (el del equipo 1) para calcular las tazas de caldo de pollo. Pregunte al grupo como se resuelve la division 6 ÷ 5 utilizando números fraccionarios. En especial, como se resuelve la division  ÷ 5 con números
fraccionarios. ÷ 5 con números
fraccionarios.
Pídales que comparen sus resultados en la tercera columna con los que escribieron en la sección Consideremos lo siguiente y corrijan si no obtuvieron lo mismo. Si los alumnos no encuentran la respuesta a la pregunta d) no se preocupe, continúen resolviendo y déjenla en blanco. |

Respuestas.
|

Propósito de la actividad. En esta
tabla se explicita la aplicación de las
dos constantes, pero en orden inverso
a la tabla anterior: primero por 8
y luego entre 5 (que también es lo
mismo que multiplicar por 
Respuestas.
|

Respuestas. Ambos métodos son
correctos, porque da lo mismo:
Si dejaron los incisos d en blanco, contéstenlos ahora. |

Sugerencia didáctica. Después
de leer esta informacion, pida a los
alumnos que prueben con varios
números para ver si efectivamente da
lo mismo multiplicar por  que dividir
entre 5 y multiplicar por 8 o viceversa. que dividir
entre 5 y multiplicar por 8 o viceversa. |

| Integrar al portafolios. En esta
sección los alumnos ponen en práctica
lo que aprendieron anteriormente.
Si todavía no han comprendido en
qué consiste la composición de dos
constantes de proporcionalidad,
resuelvan juntos la sección Manos
a la obra.
Respuestas.
|
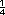 cada una de las
medidas originales. Seran 4 cm de
largo por 2 cm de alto.
cada una de las
medidas originales. Seran 4 cm de
largo por 2 cm de alto.